一个不能少!2小时断指再植术让手指重新“活”过来
来源:球友会 更新时间:2024-04-25 09:19:37
扬子晚报网4月23日讯(通讯员 景骁轶 记者 万凌云) “医生,活麻烦接上我的个不过手指……”患者岳师傅痛苦地不停呻吟着。48岁丹阳某厂工人岳师傅,再植重新因做工时不慎被钢板砸伤右手,术让手致使右手食指末节完全离断,活因伤势较严重,个不过在当地辗转几家医院无法医治,再植重新经人介绍慕名赶到镇江市中医院手足外科进行急救。术让手

问诊

门诊
一个不能少!4月23日,个不过记者从院方获悉,再植重新目前岳师傅的术让手伤指血液循环良好,毛细血管反应良好,活皮温良好。个不过在院方的再植重新努力下,再植手指存活良好。
镇江市中医院手足外科主任马文峰回忆说,4月11日下午,岳师傅在工厂负责人及工友送来时离断指体挫伤较重,整个手指末节完全掉落,断指再植难度很大。考虑到患者伤势严重,且右手食指又是功能指,接指手术刻不容缓,必须抢夺断指再植的“黄金时间”。
随即,马主任一面安抚患者,一面查看断指情况。离断指体是一种挤压、撕脱离断伤,软组织条件极差,并且离断部位在指尖,此处血管径平均约0.4mm-0.7mm。再植成活难度极大,成活率不足10%。但面对患者的请求,有着多年再植经验的手外科团队决定尽力一试。
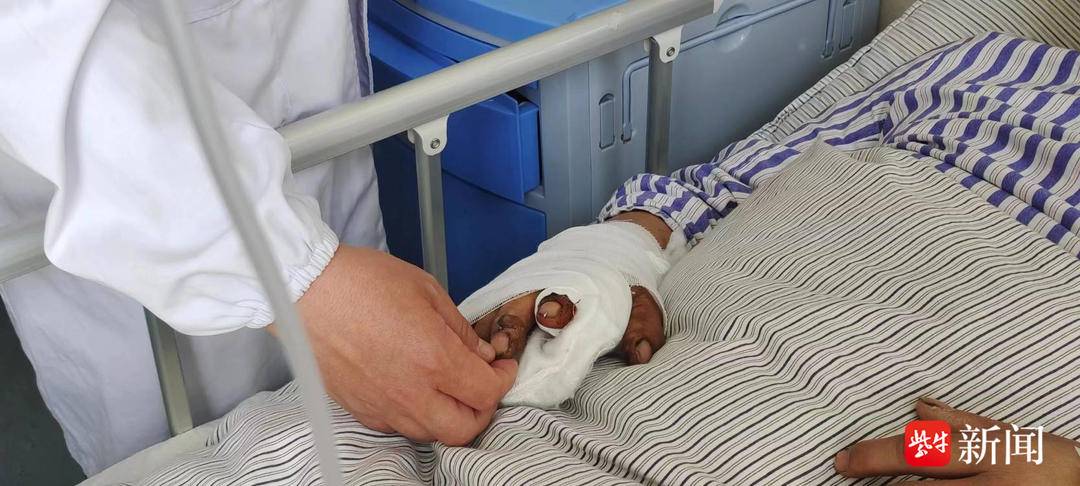
断指复活

快速确定方案,无影灯下,彻底清创、固定骨骼、修复断裂的肌腱、手术显微镜下探查血管、接通血管……马主任说,在2个小时的手术过程中,决定成败最重要的一点就是高质量的血管吻合。期间,为了缓解患者心理压力,他们不断与患者沟通,告诉他手术的情况。当血管再通成功,右示指红润,血运良好,岳师傅悬着的心终于落定。
术后,治疗团队仍不放心,每隔1小时观察血运情况,用肝素棉球湿敷,让再植的手指保持流血状态。经过手足外科医护人员的努力、患者的配合,再植指体“复活”了!
马主任提醒,断指再植具有时限性。一般来说,断指再植时间越早,成活率越高。故此,一旦发生“断指”,需要正确处理:
首先,急救的同时一定要找到断指。比如在工厂发生事故,如果断指仍在机器中,切勿强行将其拉出或将机器倒转,以免增加损伤,应立即停止机器,设法拆开机器,将断指取出,用清洁的布料包好,外面再包裹上一层后,放入干净的袋子里,有条件的可以在袋内放入冰块降温保存,并尽快送医治疗。
再者,处理断指,进行止血。当手指未完全离断,仍有一点皮肤或组织相连,其中会有细小血管提供营养,避免手指坏死,此时应妥善包扎保护固定。
其次,不完全性断指(肢),应进行有效固定。将其放在夹板上固定,迅速送医进行急救处理。
最后,以干燥冷藏方式保存断指,禁止用水或消毒液冲洗、浸泡,最好是用干净的纱布包好,6—8小时内送到医院治疗。
校对 徐珩
